Publications

Quickly discover relevant papers by filtering or searching.
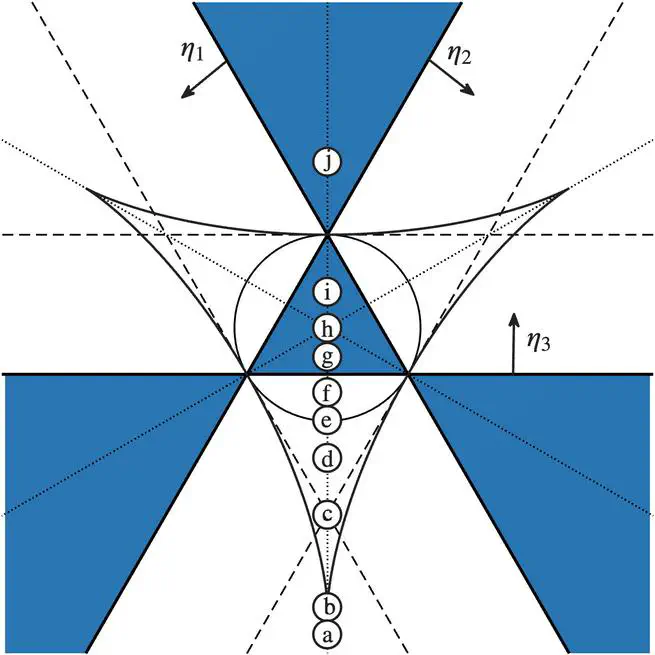
The Global Phase Space of the Three-Vortex Interaction System
The Global Phase Space of the Three-Vortex Interaction System

We derive a symplectic reduction of the evolution equations for a system of three point vortices and use the reduced system to succinctly explain a kind of bifurcation diagram that has appeared in the literature in a form that was difficult to understand and interpret. The reduction proceeds in two steps: a reduction to Jacobi coordinates and a Lie-Poisson reduction.

Apr 22, 2025
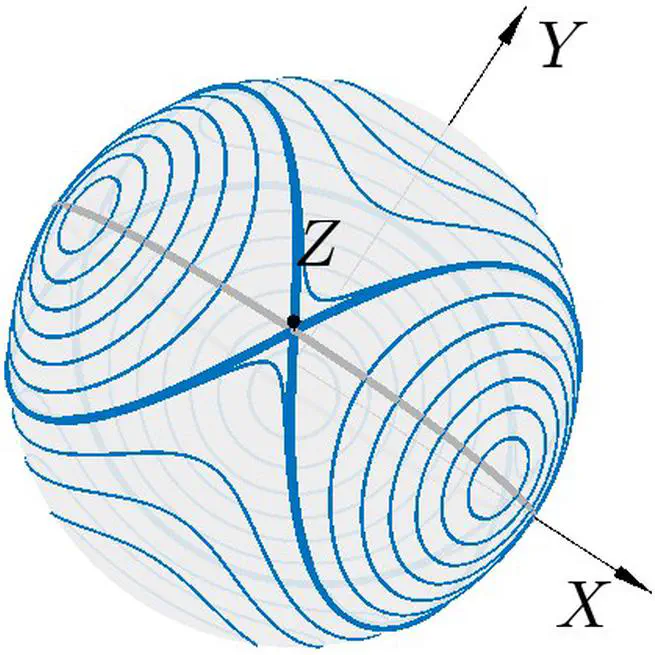
A new canonical reduction of three-vortex motion and its application to vortex-dipole scattering
A new canonical reduction of three-vortex motion and its application to vortex-dipole scattering

We use Jacobi coordinates and Nambu brackets to derive a new representation of the motion of three vortices which, unlinke all previous reductions, introduces no singularities into the system. We use this to study the scattering of dipoles by stationary vortices.

Jun 6, 2024