Generalization of Leapfrogging Orbits of Point Vortices
Jul 20, 2023·
 ·
0 min read
·
0 min read
Atul Anurag (अतुल अनुराग)
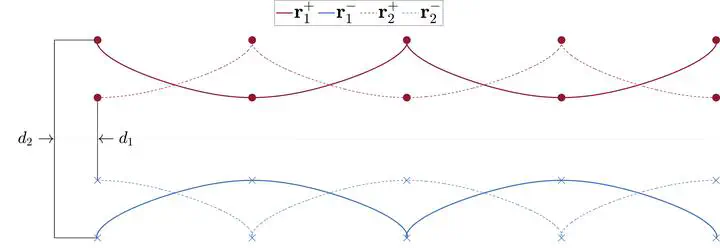 Image credit: ROY
Image credit: ROY
Abstract
Point vortex motion arises in the study of concentrated vorticity in an ideal, incompressible fluid described by Euler’s equations. The two-dimensional Euler equations of fluid mechanics, a partial differential equation (PDE) system, support a solution where the vorticity is concentrated at a single point. Helmholtz derived a system of ordinary differential equations (ODEs) that describe the motion of a set of interacting vortices that behave as discrete particles, which approximates the fluid motion in the case that the vorticity is concentrated in very small regions. This system of equations has continued to provide interesting questions for over 150 years.
We will discuss the special class of relative periodic orbits known as the leapfrogging orbits. The relative periodic of a four-point vortex problem, two positive and two negative point vortices, all of the same absolute circulation arranged as co-axial vortex pairs, is known as the leapfrogging orbit. This dissertation will present the generalizations to the leapfrogging motion of point vortices and vortex rings, including their stability and dynamics. More specifically, we will study the leapfrogging motion of 2N vortices, with circulations half positive and half negative.
We will discuss the special class of relative periodic orbits known as the leapfrogging orbits. The relative periodic of a four-point vortex problem, two positive and two negative point vortices, all of the same absolute circulation arranged as co-axial vortex pairs, is known as the leapfrogging orbit. This dissertation will present the generalizations to the leapfrogging motion of point vortices and vortex rings, including their stability and dynamics. More specifically, we will study the leapfrogging motion of 2N vortices, with circulations half positive and half negative.
Event
Location
NJIT Cullimore Hall
323 Dr Martin Luther King Jr Blvd, Newark, NJ 07102