The Phase Space of the Three-Vortex Problem
Jun 24, 2024·
·
0 min read
Atul Anurag (अतुल अनुराग)
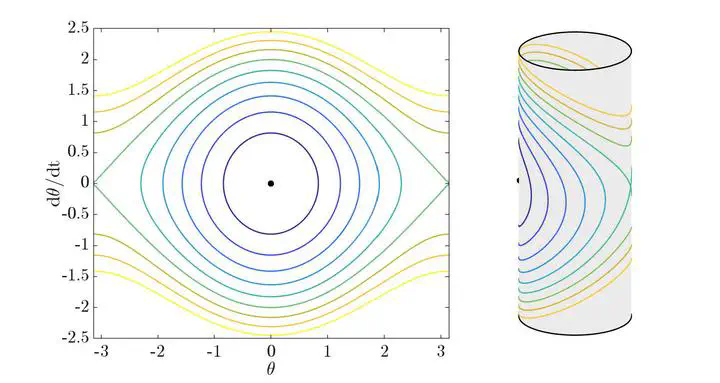Image credit: SIAM
Abstract
The motion of three point-vortices in a 2D inviscid, incompressible fluid has been widely studied. Gröbli (1877) derived a closed system for the evolution of the side lengths of the triangle formed by the vortices. This system has been the basis of most studies of this problem.
These coordinates have a few disadvantages. First, the coordinates must satisfy the triangle inequality, so not all points in $\mathbb{R}^{3}$ are physical. Second, the system introduced non-physical singularities because collinear arrangements lie on the boundary of the triangle inequality. Third, these coordinates break the useful Hamiltonian structure and make phase-plane reasoning difficult.
We introduce a coordinate system for this problem that overcomes these disadvantages using a sequence of systematic and standard reductions. We first use Jacobi coordinates, a common technique in n-body systems, and further apply a Nambu Bracket reduction. The method avoids creating non-physical singularities and makes the system’s phase-space geometry and topology plain.
A previous Nambu-bracket formulation based on Gröbli’s reduction inherited its triangle-inequality-related disadvantages. Depending on the circulations, the phase space may be a sphere or one sheet of a two-sheeted hyperboloid. Prior attempts to classify the dynamics focused solely on the stability of the relative fixed points; this approach allows us to explain the results more clearly using the entire phase space.
These coordinates have a few disadvantages. First, the coordinates must satisfy the triangle inequality, so not all points in $\mathbb{R}^{3}$ are physical. Second, the system introduced non-physical singularities because collinear arrangements lie on the boundary of the triangle inequality. Third, these coordinates break the useful Hamiltonian structure and make phase-plane reasoning difficult.
We introduce a coordinate system for this problem that overcomes these disadvantages using a sequence of systematic and standard reductions. We first use Jacobi coordinates, a common technique in n-body systems, and further apply a Nambu Bracket reduction. The method avoids creating non-physical singularities and makes the system’s phase-space geometry and topology plain.
A previous Nambu-bracket formulation based on Gröbli’s reduction inherited its triangle-inequality-related disadvantages. Depending on the circulations, the phase space may be a sphere or one sheet of a two-sheeted hyperboloid. Prior attempts to classify the dynamics focused solely on the stability of the relative fixed points; this approach allows us to explain the results more clearly using the entire phase space.
Event
Location
Lord Baltimore Hotel
20 W Baltimore St, Baltimore, MD 21201
